Glossary

Section author: Frédéric Richard <frederic.richard_at_univ-amu.fr>

random field

A random field \(Z\) is a collection of random variables \(Z(x)\) which are located at positions \(x\) of a multidimensional space (for instance, the plane \(\mathbb{R}^2\)). A collection of variables defined on \(\mathbb{R}\) is rather called a random process.

The random field is Gaussian if any linear combination \(\sum_{i=1}^n \lambda_i Z(x_i)\) is a Gaussian random variable. The probability distribution of a Gaussian field is characterized by

• its expectation function:

  \[x \rightarrow \mathbb{E}(Z(x)),\]

• its covariance function:

  \[(x, y) \rightarrow \mathrm{cov}(Z(x), Z(y)).\]

stationarity

A random field \(Z\) is (second-order) stationary if \(\mathbb{E}(Z(x))\) does not depend on the position \(x\) (is constant) and if \(\mathrm{cov}(Z(x), Z(y))\) only depends on the relative position \(x-y\). First and second-order properties of such a field are the same all over the space.

increments

Increments \(W\) (of order 0) of a random field \(Z\) are random variables of the form

\[W = \sum_{i=1}^n \lambda_i Z(x_i),\]

where \(\lambda_i\) are such that \(\sum_{i=1}^n \lambda_i =0\). For instance, \(Z(x+h) - Z(x)\) is an increment of \(Z\). More generally, increments of order \(k \in \mathbb{N}\) are increments such that \(\sum_{i=1}^n \lambda_i P(x_i) =0\) for any polynomial \(P\) of order \(k\).

An increment field \(W\) is a set of increments \(W(y)\) defined at any position \(y\) by

\[W(y) = \sum_{i=1}^n \lambda_i Z(y + x_i).\]

intrinsic

An intrinsic random field of order \(k\) is a random field whose increments of order \(k\) are stationary [3, 4, 5, 6, 7, 12]. An intrinsic field of order 0 is simply called random fields with stationary increments.

semi-variogram

Let \(Z\) be a random field with stationary increments. The semi-variogram of \(Z\) is defined, for any \(h\), by

\[v(h) = \frac{1}{2} \mathbb{E}((Z(h) - Z(0))^2) = \frac{1}{2} \mathbb{E}((Z(x+h) - Z(x))^2), \forall x.\]

density

Let \(Z\) be a random field with stationary increments. A non-negative and even function \(f\) is the density of \(Z\) if

\[v(h) = \int_{\mathbb{R}^2} \vert e^{i\langle w, h\rangle} -1 \vert^2 f(w) dw,\]

The density of an AFBF is of the form

\[f(w)=\tau(\arg(w)) |w|^{-2\beta(\arg(w))-2}, w \in \mathbb{R}^2,\]

where \(\tau\) and \(\beta\) are non-negative \(\pi\)-periodic functions depending both on the direction \(\arg(w)\) of the frequency \(w\).

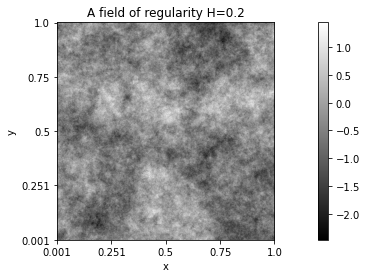
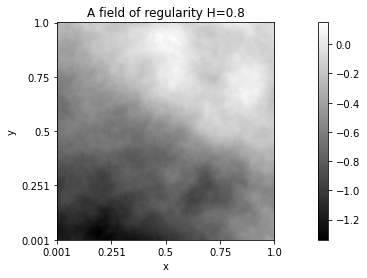
regularity

The regularity (in the Hölder sense) of a random field \(Z\) is the highest value \(H \in (0, 1)\) for which

\[\vert Z(y) - Z(x) \vert \leq c \vert y - x \vert^\alpha\]

holds with probability 1 for any \(\alpha < H\) and \(x, y\) in any arbitrary compact set.

isotropy

A field is isotropic if its properties are the same in all space directions. A Gaussian random field with stationary increments and density \(f\) is isotropic if and only if \(f\) is radial, ie.

\[f(w) = \tilde{f}(\vert w \vert), \forall w,\]

meaning that values of \(f\) does not depend on the direction \(\arg(w)\) of \(w\), but only on its module \(\vert w \vert\).

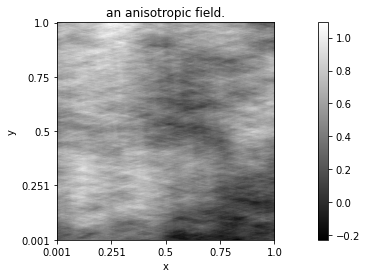
A field is anisotropic if it is not isotropic.

The difference between realizations of isotropic and anisotropic fields is illustrated below.