Heterogeneous textures from local deformation

Code author: Frédéric Richard <frederic.richard_at_univ-amu.fr>

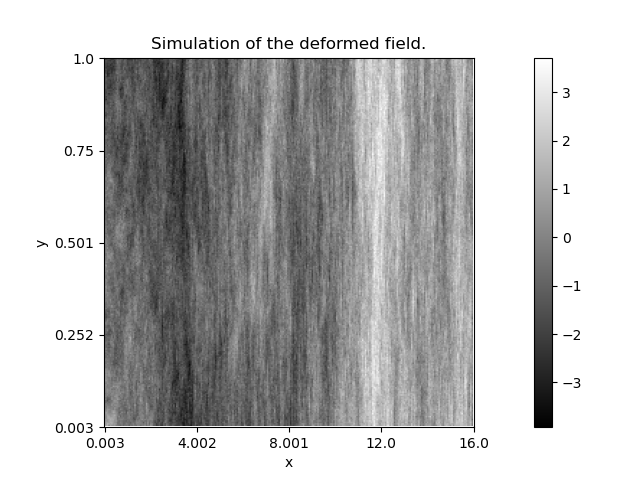
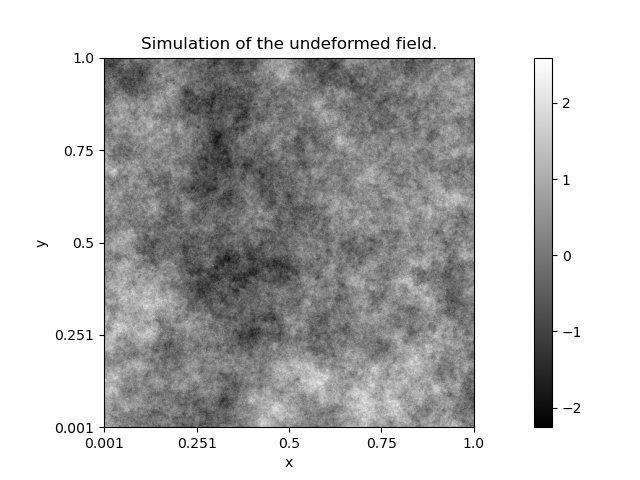
In this example, we show how to simulate heterogeneous textures by applying a local deformation to an isotropic random field.

Given a fractional Brownian field \(X\), the transformed field is defined by composition

\[Y = X \circ T,\]

of \(X\) with a transformation \(T\) mapping \((x, y)\) into \((x^{1.5}, y)\).

The heterogeneous texture is obtained by simulation of \(Y\).

Note

Such an approach can only be applied if the transformed coordinates remain integer.

• 
• 

import numpy as np
from afbf import coordinates, tbfield

# Define a fractional Brownian field.
X = tbfield()
# Define an affine transform.
T = np.array([[1, 0], [2, 1]], dtype=int)

# Define a uniform grid.
coord = coordinates(256)
# Simulate the field without transformation.
n0 = int(np.random.randn())
np.random.seed(1)
y0 = X.Simulate()

# Apply a local transform to the the grid.
coord.xy[:, 0] = np.power(coord.xy[:, 0], 1.5)
# Simulate the field with transformation (with a same seed).
y = X.Simulate(coord)

# Display of simulations.
y.name = 'Simulation of the deformed field.'
y.Display(1)

y0.name = 'Simulation of the undeformed field.'
y0.Display(2)